backtracking for rare case when sun below tracker improvement

[mikofski]

Describe the bug

• related to singleaxis tracking: backtracking error #656
• in the rare case when the sun rays are below the tracker, then the top of the next row is shaded
• currently tracker backtracks away from sun, back is facing sun instead of front
• this only happens for tilted trackers and very low sun angles, either early morning or late evening when the sun rays are furthest north or south

To Reproduce
Steps to reproduce the behavior:

1. create a tilted tracker

# in Brazil so facing north
axis_azimuth = 0.0 
axis_tilt = 20
max_angle = 75.0
gcr = 0.35

2. pick the earliest morning (or latest evening) timestamp

import pvlib
import pandas as pd

# Brazil, timezone is UTC-3[hrs]
starttime = '2017-01-01T00:30:00-0300'
stoptime = '2017-12-31T23:59:59-0300'
lat, lon = -27.597300, -48.549610
times = pd.DatetimeIndex(pd.date_range(
    starttime, stoptime, freq='H'))
solpos = pvlib.solarposition.get_solarposition(
    times, lat, lon)
# get the early times
ts0 = '2017-01-01 05:30:00-03:00'
ts1 = '2017-01-01 12:30:00-03:00'
apparent_zenith = solpos['apparent_zenith'][ts0:ts1]
azimuth = solpos['azimuth'][ts0:ts1]
sat = pvlib.tracking.singleaxis(
    apparent_zenith, azimuth, axis_tilt, axis_azimuth, max_angle, True, gcr)

3. notice that the tracker suddenly jumps from one side facing east to west

                           tracker_theta        aoi  surface_azimuth  surface_tilt
2017-01-01 05:30:00-03:00     -21.964540  62.721237       310.299287     29.368272
2017-01-01 06:30:00-03:00      16.231156  69.264752        40.403367     25.546154
2017-01-01 07:30:00-03:00      69.073645  20.433849        82.548858     70.389280
2017-01-01 08:30:00-03:00      54.554616  18.683626        76.316479     56.978562
2017-01-01 09:30:00-03:00      40.131687  17.224233        67.917292     44.072837
2017-01-01 10:30:00-03:00      25.769332  16.144347        54.683567     32.194782
2017-01-01 11:30:00-03:00      11.439675  15.509532        30.610665     22.923644
2017-01-01 12:30:00-03:00      -2.877428  15.358209       351.639727     20.197537

4. AOI is also wrong

Expected behavior
The tracker should avoid shade. It should not jump from one direction to the other. If the sun ray is below the tracker then it will need to track to it's max rotation or backtrack. If there is shading at it's max rotation then it should track backtrack to zero, or perhaps parallel to the sun rays. Perhaps if bifacial, then it could go backwards, 180 from the correct backtrack position to show it's backside to the sun.

proposed algorithm (updated after this comment):

if backtracking:
    # cos(R) = L / Lx, R is rotation, L is surface length,
    # Lx is shadow on ground, tracker shades when Lx > x
    # x is row spacing related to GCR, x = L/GCR
    lrot = np.cos(tr_rot_no_lim)  # tracker rotation not limited by max angle

    # Note: if tr_rot > 90[deg] then lrot < 0 
    # which *can* happen at low angles if axis tilt > 0
    # tracker should never backtrack more than 90[deg], when lrot = 0
    cos_rot = np.minimum(np.abs(lrot) / self.gcr, 1)

    # so if lrot<0 tracker should backtrack forward
    # backtrack_rot = np.sign(lrot) * np.arccos(cos_rot)

    # NOTE: updated after comment from @kevinsa5 at Nov 27, 2019, 8:16 AM PST
    # to remove sign()
    backtrack_rot = np.arccos(cos_rot)

also remove abs from aoi calculation

pvlib-python/pvlib/tracking.py

Line 461 in c699575

aoi = np.degrees(np.arccos(np.abs(np.sum(sun_vec*panel_norm, axis=0))))

Screenshots
If applicable, add screenshots to help explain your problem.

Versions:

• pvlib.__version__: 0.6.3
• pandas.__version__: 0.24
• python: 3.7

Additional context
Add any other context about the problem here.

[cwhanse]

Related to #65 is a typo? I'm not following step 1, what is system_plane defining?

[mikofski]

Thanks, I updated the description to reference #656, sorry.

oops re: system plane, that's related to the new PR, #823, it's the plane that contains all the trackers, but it isn't necessary here, because we can have this same issue on a tilted tracker that is parallel to the slope (system plane) it's on.

[mikofski]

PTAL @kevinsa5 thx!

[kevinsa5]

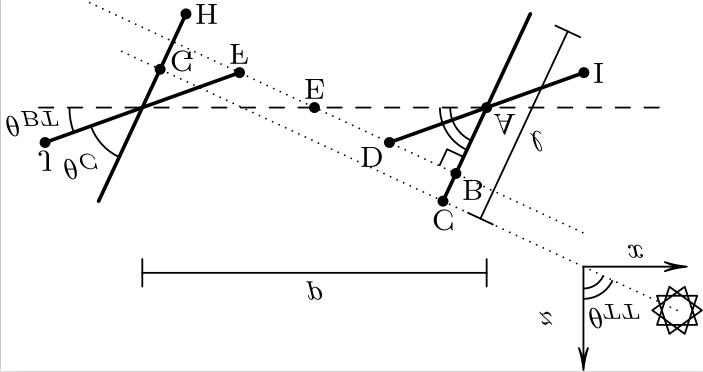
To make sure I understand the geometry -- here's a sideview truetracking vs backtracking diagram I have laying around, so apologies for the extraneous labeling. The math behind "normal" backtracking when the sun is above the array is to align points C and H (or D and F, with backtracking enabled) such that their tangent line is parallel to the sun's rays. This tangent line coincides with the edge of the shadow cast by the row in front. As the sun crosses the system plane (dashed line) and passes "underneath" the array, each row's shadow crosses over the row behind it, which means that the relevant shadow edge switches -- instead of aligning points D and F, the goal is now to align points I and J. As such, the correct backtracking behavior is for tracker angle to momentarily touch zero right when the sun crosses the system plane, then to increase again until sun is below horizon (or max angle is reached). For instance, if position I-D in the figure represents the correct backtracking angle for some solar position where the sun is above the array as it sets, the row should proceed to track flatter until the sun crosses the dashed line, and then reverse course back to I-D and beyond as the sun continues to drop below the plane.

@mikofski does that sound right?

[mikofski]

Thanks so much for commenting!

and then reverse course back to I-D and beyond as the sun continues to drop below the plane.

Yes this is what I am also suggesting.

Maybe it's easier to visualize if we flip the sketch, unfortunately you also have to mentally switch I & D if you want the front of the PV surface to face the sun:

Interesting, from this perspective, it appears that at the instant after the sun crosses the "system" plane and the sun drops below it, the PV surface if backtracking would have to flip 180[deg] forward in order to face downward at the sun, but then would rotate back again as the true tracking position continued forward until backtracking was no longer necessary.

So I think my proposed algorithm is correct:

• sat is the current backtracking algorithm
• sat180no is no backtracking with max angle at 180[deg]
• tracker_wbacktrack is the proposed backtracking algorithm

1. before 6am, the backtracking is in front of the tracker, so the tracker forward-tracks to avoid shade
2. around 6am the tracker is at 180[deg] and the tracker is near 90[deg] rotation
3. between 6 and 6:05am the tracker jumps from 180[deg] to 0[deg]
4. after 6:05am, the two algorithms agree

Expand to see code...

import pvlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# in Brazil so facing north
axis_azimuth = 0.0 
axis_tilt = 20
max_angle = 75.0
gcr = 0.35

# Brazil, timezone is UTC-3[hrs]
starttime = '2017-01-01T00:30:00-0300'
stoptime = '2017-12-31T23:59:59-0300'
lat, lon = -27.597300, -48.549610
times = pd.DatetimeIndex(pd.date_range(
    starttime, stoptime, freq='5T'))
solpos = pvlib.solarposition.get_solarposition(
    times, lat, lon)

# get the early times
ts0 = '2017-01-01 05:30:00-03:00'
ts1 = '2017-01-01 12:30:00-03:00'
apparent_zenith = solpos['apparent_zenith'][ts0:ts1]
azimuth = solpos['azimuth'][ts0:ts1]

# current implementation
sat = pvlib.tracking.singleaxis(
    apparent_zenith, azimuth, axis_tilt, axis_azimuth, max_angle, True, gcr)

# turn off backtracking and set max angle to 180[deg]
sat180no = pvlib.tracking.singleaxis(
    apparent_zenith, azimuth, axis_tilt, axis_azimuth, max_angle=180, gcr=gcr, backtrack=False)

# calculate cos(R)
# cos(R) = L / Lx, R is rotation, L is surface length,
# Lx is shadow on ground, tracker shades when Lx > x
# x is row spacing related to GCR, x = L/GCR
lrot = np.cos(np.radians(sat180no.tracker_theta))

# proposed backtracking algorithm for sun below trackers
# Note: if tr_rot > 90[deg] then lrot < 0 
# which *can* happen at low angles if axis tilt > 0
# tracker should never backtrack more than 90[deg], when lrot = 0
cos_rot = np.minimum(np.abs(lrot) / gcr, 1.0)
backtrack_rot = np.sign(lrot) * np.degrees(np.arccos(cos_rot))
tracker_wbacktrack = sat180no.tracker_theta - np.sign(sat180no.tracker_theta) * backtrack_rot

# plot figure
df = pd.DataFrame({
'sat': sat.tracker_theta,
'sat180no': sat180no.tracker_theta,
'lrot': lrot,
'cos_rot': cos_rot,
'backtrack_rot': backtrack_rot,
'tracker_wbacktrack': tracker_wbacktrack})
plt.ion()
df[['sat', 'sat180no', 'tracker_wbacktrack']].iloc[:25].plot()
plt.title('proposed backtracking for sun below tracker')
plt.ylabel('tracker rotation [degrees]')
plt.yticks(np.arange(-30,200,15))
plt.grid()

[kevinsa5]

I'm not sure that this point is necessarily true:

it appears that at the instant after the sun crosses the "system" plane and the sun drops below it, the PV surface if backtracking would have to flip 180[deg] forward in order to face downward at the sun

From my understanding, there are two backtracking positions that eliminate row-to-row shading and present the same cross section to incoming beam irradiance. In the below diagram (another that I already had laying around), the sun has crossed below the system plane and it shows the two possible backtracking positions. P1 is what you're describing where the front face of the module has rotated around and is now facing backwards/down and P2 is what I tried to describe above where the modules are still facing forwards/up. I believe the two are equivalent in terms of DNI collection and shading, but the forwards/up variant would presumably have better diffuse collection and is more accommodating of tracker rotation limits.

I don't have the math already coded up for this so I can't generate a comparison plot of tracker angle, but I think it would look something like the absolute value of your blue line -- a moment where tracker_angle=0 when the sun crosses the system plane, with positive tracker angle on both sides of the zero.

[mikofski]

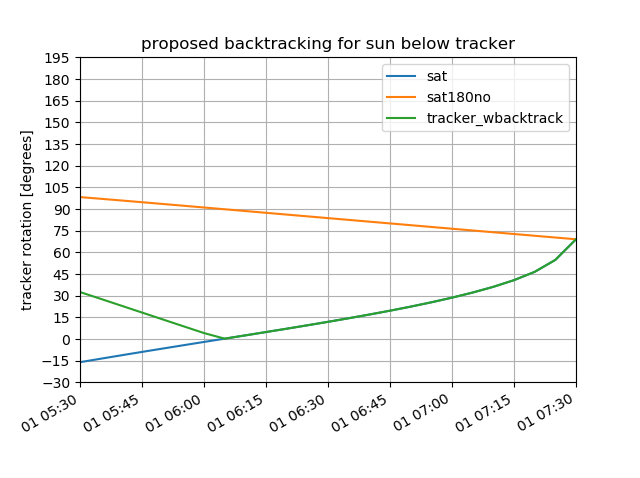
Excellent insight! I agree, and I think your proposal is much better!!

Here's what I get now:

I just made the one change you suggested to take absolute value, actually because abs(lrot) was already in there, I just removed the sign(backtrack_rot) (click to expand):

import pvlib
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# in Brazil so facing north
axis_azimuth = 0.0 
axis_tilt = 20
max_angle = 75.0
gcr = 0.35

# Brazil, timezone is UTC-3[hrs]
starttime = '2017-01-01T00:30:00-0300'
stoptime = '2017-12-31T23:59:59-0300'
lat, lon = -27.597300, -48.549610
times = pd.DatetimeIndex(pd.date_range(
    starttime, stoptime, freq='5T'))
solpos = pvlib.solarposition.get_solarposition(
    times, lat, lon)

# get the early times
ts0 = '2017-01-01 05:30:00-03:00'
ts1 = '2017-01-01 12:30:00-03:00'
apparent_zenith = solpos['apparent_zenith'][ts0:ts1]
azimuth = solpos['azimuth'][ts0:ts1]

# current implementation
sat = pvlib.tracking.singleaxis(
    apparent_zenith, azimuth, axis_tilt, axis_azimuth, max_angle, True, gcr)

# turn off backtracking and set max angle to 180[deg]
sat180no = pvlib.tracking.singleaxis(
    apparent_zenith, azimuth, axis_tilt, axis_azimuth, max_angle=180, gcr=gcr, backtrack=False)

# calculate cos(R)
# cos(R) = L / Lx, R is rotation, L is surface length,
# Lx is shadow on ground, tracker shades when Lx > x
# x is row spacing related to GCR, x = L/GCR
lrot = np.cos(np.radians(sat180no.tracker_theta))

# proposed backtracking algorithm for sun below trackers
# Note: if tr_rot > 90[deg] then lrot < 0 
# which *can* happen at low angles if axis tilt > 0
# tracker should never backtrack more than 90[deg], when lrot = 0
# if sun below trackers then use abs() to reverse direction of trackers
cos_rot = np.minimum(np.abs(lrot) / gcr, 1.0)
backtrack_rot = np.degrees(np.arccos(cos_rot))

# combine backtracking correction with the true-tracked rotation
# Note: arccosine always positive between [-90, 90] so change
# sign of backtrack correction depending on which way tracker is rotating
tracker_wbacktrack = sat180no.tracker_theta - np.sign(sat180no.tracker_theta) * backtrack_rot

# plot figure
df = pd.DataFrame({
'sat': sat.tracker_theta,
'sat180no': sat180no.tracker_theta,
'lrot': lrot,
'cos_rot': cos_rot,
'backtrack_rot': backtrack_rot,
'tracker_wbacktrack': tracker_wbacktrack})
plt.ion()
df[['sat', 'sat180no', 'tracker_wbacktrack']].iloc[:25].plot()
plt.title('proposed backtracking for sun below tracker')
plt.ylabel('tracker rotation [degrees]')
plt.yticks(np.arange(-30,200,15))
plt.grid()

[mikofski]

Here is a visual double check that this does what we want using Shapely:

• at 5:30 AM the sun is below the tracker "system" plane and shades the top of the next tracker (magenta dashed line)
• the true track rotation at 5:30 AM is 98.7[deg]
• the proposed backtrack rotation is 32.5[deg], facing up and toward the sun (tracker 1: gray, tracker 2: greenish-yellow)
• the current backtrack rotation is -16[deg], so facing up but away from sun (tracker 1: blueish, tracker 2: orange)
• an alternate, but suboptimal rotation is 164[deg, so facing down but toward the sun
• the parallel sunray (light blue dashed) does not shade either backtracking option

Just tack on this code the bottom of the snippet (click to exp and, also at this gist):

from shapely.geometry.polygon import LinearRing
from shapely import affinity
from shapely.geometry import LineString

L = 1.6  # length of trackers
P = L/gcr  # distance between rows

f = plt.figure('trackers')  # new figure

# true track position at 5:30AM
tracker_theta = -np.radians(df.sat180no.values[0])

# tracker 1 circle
pts1 = np.radians(np.arange(360))
pts1 = np.stack((L/2*np.cos(pts1), L/2*np.sin(pts1)), axis=1)
circle1 = LinearRing(pts1)
plt.plot(*circle1.xy, ':')

# tracker 2 circle
pts2 = np.radians(np.arange(360))
pts2 = np.stack((P + L/2*np.cos(pts2), L/2*np.sin(pts2)), axis=1)
circle2 = LinearRing(pts2)
plt.plot(*circle2.xy, ':')

# tracker 1 surface
tracker1 = LineString([(-L/2, 0), (L/2, 0)])
plt.plot(*tracker1.xy, '-.')
tracker1rot = affinity.rotate(
    tracker1, tracker_theta, use_radians=True)
plt.plot(*tracker1rot.xy)

# tracker 2 surface
tracker2 = LineString([(P-L/2, 0), (P+L/2, 0)])
plt.plot(*tracker2.xy, '-.')
center2 = shapely.geometry.Point((P, 0))
tracker2rot = affinity.rotate(
    tracker2, angle=tracker_theta, use_radians=True, origin=center2)
plt.plot(*tracker2rot.xy)

# sunray
a, b = tracker2rot.coords
d0 = b[0] - P
d1 = b[1] - P * np.tan(tracker_theta-np.pi/2)
sunray2 = LineString([b, (d0, d1)])
plt.plot(*sunray2.xy, '--')

# backtracking
tracker_theta = -np.radians(df.tracker_wbacktrack.values[0])

# backtrack tracker 1 surface
tracker1 = LineString([(-L/2, 0), (L/2, 0)])
tracker1rot = affinity.rotate(
    tracker1, tracker_theta, use_radians=True)
plt.plot(*tracker1rot.xy)

# tracker 2 surface
tracker2 = LineString([(P-L/2, 0), (P+L/2, 0)])
center2 = shapely.geometry.Point((P, 0))
tracker2rot = affinity.rotate(
    tracker2, angle=tracker_theta, use_radians=True, origin=center2)
plt.plot(*tracker2rot.xy)

# parallel sunrays
sun_angle1 = np.arctan2(*reversed(np.diff(sunray1.xy)))
# sun_angle2 = np.arctan2(*reversed(np.diff(sunray2.xy)))
a, b = tracker1rot.coords
c0 = a[0] + P + L
c1 = a[1] + (P+L) * np.tan(sun_angle1)
sunray1 = LineString([a, (c0, c1)])
plt.plot(*sunray1.xy, '--')

# alternate backtracking
tracker_theta = -np.radians(df.sat.values[0])

# backtrack tracker 1 surface
tracker1 = LineString([(-L/2, 0), (L/2, 0)])
tracker1rot = affinity.rotate(
    tracker1, tracker_theta, use_radians=True)
plt.plot(*tracker1rot.xy)

# tracker 2 surface
tracker2 = LineString([(P-L/2, 0), (P+L/2, 0)])
center2 = shapely.geometry.Point((P, 0))
tracker2rot = affinity.rotate(
    tracker2, angle=tracker_theta, use_radians=True, origin=center2)
plt.plot(*tracker2rot.xy)

plt.gca().axis('equal')
plt.ylim([-2,6])
plt.xlim([-2,6])
plt.grid()
plt.title('Backtracking with sun below trackers')
plt.xlabel('distance between rows')
plt.ylabel('height above "system" plane')
plt.legend([
    'tracker 1',
    'tracker 2',
    'tracker 1: system plane',
    'tracker 1: true track 98.3[deg]',
    'tracker 2: system plane',
    'tracker 2: true track 98.3[deg]',
    'sunray',
    'tracker 1: backtrack 32.5[deg]',
    'tracker 2: backtrack 32.5[deg]',
    'parallel sunray',
    'tracker 1: alt backtrack -16[deg] or 164[deg]',
    'tracker 2: alt backtrack -16[deg] or 164[deg]'])

[kevinsa5]

Yep, I think we're on the same page now. I like the results your code gives in the morning, but I'm getting bad results in the evening, I believe because of a combination of two things: pvlib returns truetracking angles in [-90,+270] (see the responsible line of code) which means sat180no angle rolls over to +270 towards the end of the day. Then max_angle=180 clips the truetracking angle to +180 and messes up lrot as a result. I believe changing max_angle to 360 and remapping to [-180,+180] makes the afternoon work as well in your code. So in short, I think this only needs two modifications to the current pvlib implementation:

• insert after Line 422: wid = (wid+180) % 360 - 180 or equivalent
• modify Line 433 to use the absolute value of cosd(wid)

Does that look right?

A couple other thoughts:

• Would it be worthwhile to include an option to swap between the two backtracking strategies (traditional backtracking vs what could be called "overtracking")? I'm not sure "overtracking" is ever preferable -- the only thing that comes to mind is if you'd rather face the modules down instead of up, for instance on the moon where there's ground diffuse but no sky diffuse...
• It strikes me as a little cleaner to explicitly calculate when backtracking should be active instead of forcing the correction to zero via max/min to [-1,+1]. Something like backtrack_condition = np.cos(np.radians(truetracking_theta)) < gcr. Just a minor personal preference.